Mastermind
Code for this project can be found here.
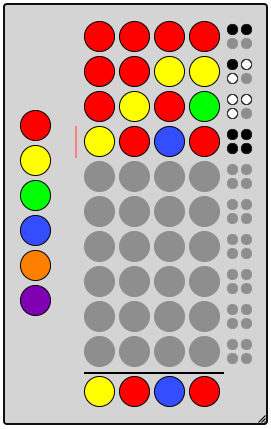
An example game of Mastermind
Mastermind is the classic predecessor to the incredibly popular Wordle. In Mastermind, you guess sequences of colors rather than 5 letter words. You then get a response with black pegs for each correct color in the correct position and white pegs for any remaining correct colors in an incorrect position.
To represent the game in software, it is apparent that numbers are a more efficient choice than colors. Doing so has the added benefit of making it easier to store information of all codes in an array. A 4 digit code with 6 possible colors is just a 4 digit number in base 6.
To play Mastermind well, you need to efficiently eliminate possibilities. When you make a guess and get a response, you can eliminate all possibilities inconsistent with that guess-response pair. I chose to apply the minimax principle to this game; choose a guess so the worst case response eliminates as many candidate codes as possible. You can do this by (in concept):
For a possible guess, count how many still valid codes would give each possible response
Assign that guess a score equal to the largest count among all the possible responses
Guess the code that has the lowest score
The following galleries show how the remaining possibilities while a human is playing compare to the possibilities while the computer plays using the minimax principle.
As for implementation, the first and most obvious improvement is to cache all of the comparisons between the possible codes. This makes finding the response a simple lookup operation. There are two stages to the algorithm: picking the best guess and updating the possibilities after receiving a response. An implementation with quadratic guess selection and linear possibility updating is fairly straightforward - just implement the algorithm as described and have an auxiliary array to track which codes are still possible. When going about implementing this algorithm, I was focused on reducing the guess selection to linear complexity. I did this using a list of dictionaries, one dictionary for each code. In that dictionary, the keys were the possible responses and the values were lists of the still valid codes that would give that response. This does achieve linear guess selection because the “score” has already been computed for each code. What I did not realize at the time is that my implementation does not improve the overall performance of the algorithm. Maintaining the structure pushes the response update process to quadratic. In fact, no implementation can avoid quadratic complexity, because at some point all possible combinations of guess and true code must be considered.